uses the internal state of modern
processors, the audio entropy daemon uses
audio noise, and the video entropy daemon
noise from a camera.]
| ↑↑ Home | ↑ Science |
Obtaining data -- Randomness tests -- Extraction and correction
Random numbers are useful for many things, including numerical integration and cryptography. The simplest way of obtaining suitable numbers are pseudo-random-number generators – most operating systems provide one, and the numerics literature documents a range of algorithms.
But genuine non-deterministic random numbers are surprisingly easy to obtain too – look no further than your sound card. The analog input of today's typical sound card is digitised with enough bits that the least significant bits are just noise. If you have an audio application with a level meter (VU meter), you can observe this – the fluctuating input level displayed when you supply no signal input is the noise level. A VU meter usually displays the signal level (i.e., the squared amplitude) in dB. This means that 6 dB amount to one (amplitude) bit.
[Aside: This page describes a way to obtain random numbers from audio inputs
without administrator privileges. To increase the random number output of your
own box, there are a number of ready-made Linux packages that provide true
randomness via the kernel's random device:
haveged uses the internal state of modern
processors, the audio entropy daemon uses
audio noise, and the video entropy daemon
noise from a camera.]
To get at the noise bits, you simply record from the sound card in question. It is not necessary to connect a signal source, though it should not do any harm either. How you record sound will differ on your operating system and personal preference. On my Linux box, I use the command-line program arecord.
To obtain the noisy least significant bits, you have to record with the maximum bit width which the sound card provides. Otherwise the least significant bits will be cut off. If in doubt, record with 32 bits and look at the data afterwards to see which bits vary. For some sound cards, the digitised bit width is less than the nominal maximum bit width – for example, the Intel HDA implementation in the ICH7 chipset provides 20 significant bits but up to 32 can be recorded (with the least significant always being zero).
To be able to process the recorded data further, you should also have some basic knowledge of the audio format you record in. It should record the samples from the sound card without modification, which rules out non-linear sample encodings such as μ-law, which some formats support, let alone lossy compression such as MP3. In the following I will assume that your format stores sample values in a whole number of bytes each, like for example the common WAVE file format. You also need to know the header size of your format, in order to be able to skip it. A hexadecimal editor can be very useful to locate those bytes containing the noise bits.
Before using your audio noise bits for anything serious, you will want to be reasonably sure that they are indeed random. This is easier said than done. There is no such thing as a "proof of randomness". A number series containing a long stretch of constant numbers may result from a random process, and one that never contains such stretches definitely is not random. Testing for randomness amounts to testing for properties of random numbers which methods requiring them rely on. If you have a specific application in mind, you may have a criterion that is especially important to you, and should test for it. I have programmed a few general-purpose tests that you can download in this archive.
All the test programs below share the same syntax:
<program> <file> <skip>[.<bit>] <stride> [<channels>]
The first argument is the input file, the second gives the number of header bytes to skip and the bit to use. <stride> is the offset in bytes between successive values to extract bits from. The last, optional, argument, allows to process interleaved series of data such as stereo recordings.
This test, implemented in bit0stat.c, counts the number of samples in which a given bit (bit 0 by default) is 0 or 1. It outputs:
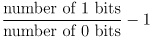
The result is a number between -1 and 1, and a positive result means an excess of 1 bits and vice versa. A zero result would indicate a perfectly uniform distribution.
Interestingly, the bit balance seems to serve as an indicator of sound card quality too. My good sound card from Echoaudio has half the imbalance (on average) as the Intel HDA sound on my mainboard.
The test program 5bitstat.c outputs a histogram of values made up of the lower 5 bits of each sample by default. If the <bit> argument is given, bits 0 to <bit>-1 are used. The program also outputs the quotient of the RMS deviation and mean of the histogram (not the values) as a measure of how flat the histogram is.
The results of this test help decide whether you can use values composed of the noise bits as they are. (That the default number of bits is 5 is just because that is the number of noise bits of one of my sound cards, and this can be changed in the source code.)
The next test program, bitcorr.c, computes the autocorrelation of the bit stream consisting of a given bit of each sample word. It outputs the autocorrelation values up to an offset of 1024 (can be changed in the source code). A value of 1 indicates perfect correlation (repetitive pattern), a value of -1 perfect anticorrelation. The RMS and absolute minimum and maximum of the correlation values is also output for a quick overview.
This and the following test make use of the ability of the human eye to spot patterns in images. The program bits2points.c composes bits from the audio file into coordinates in an image and marks the corresponding points. Points which are hit once are coloured light grey, twice dark grey, and three or more times black.
This test uses only a predefined share of the sample values, which results from the image size and a density defined in the source code. It outputs the offset of the first unused value in the audio file to allow continuing there.
This test does not provide a numerical result but requires you to decide whether the resulting image looks random. If you want a supplementary numerical measure, you can use an image processing program to compute the image histogram. (For example, use identify -verbose from the ImageMagick package.) Contrary to naive intuition, the share of points hit twice and more times are not powers of the share of points hit once. Rather, these fractions (probabilities) are:
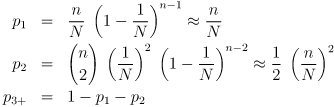
where N is the number of pixels in the image (by default 220) and n the number of coordinate pairs extracted (by default N/64). The key to this counting problem is to start from the coordinate pairs, which are statistically independent and therefore have to be treated as drawings with repetition. The expected proportion of points being hit once is the same as the probability of hitting a given, fixed point once. For p1 we need exactly one coordinate pair to hit that point, which happens with probability 1/N, and all the other (n-1) to avoid it, which gives ((N-1)/N)(n-1). For p2 two coordinate pairs have to match, and the other (n-2) have to miss. It remains to explain the binomial coefficients (n for p1) in front. Clearly they come from some kind of drawing without repetition, but not of coordinate pairs, but of the random value(s) containing the matching pair(s). The matching coordinates may occur at any point in the sequence of n random coordinate pairs, so the probabilities have to be multiplied by the corresponding multiplicities.
Like the previous test, the program bits2bitmap.c converts the noise bits to an image in which one can try to see regularities. Each bit represents one black or white pixel. Only a fixed number of sample values are used, as needed for the image size. The offset of the first unused value is output to the terminal.
My package of programs also contains a program getbit.c which extracts a given bit from all audio samples and writes them to a file. Its command-line syntax is the same as for the test programs.
If your sound card noise has a statistical bias, that can be corrected. One option is to use the same methods as for turning uniformly-distributed numbers into a different distribution, such as selection or function application. Both will require modelling the bias.
An easier way is to combine the random numbers with the output of a pseudo-random number generator, for example with a bitwise exclusive-or operation. The result retains both the statistical properties of the pseudo-random numbers and the non-determinism of the genuine random numbers, the best of both worlds. Combining genuine with pseudo-random numbers is free of the dangers of combining the output of two pseudo-random-number generators (the result may end up less random than either), so you might apply it as a precautionary measure in any case. The program xor.c in my source package can be used to do that when you have written the pseudo-random numbers to a file.